关于树的算法总结

二叉树的题目普遍可以用递归和迭代的方式解决

我的新书《LangChain编程从入门到实践》 已经开售！推荐正在学习AI应用开发的朋友购买阅读！

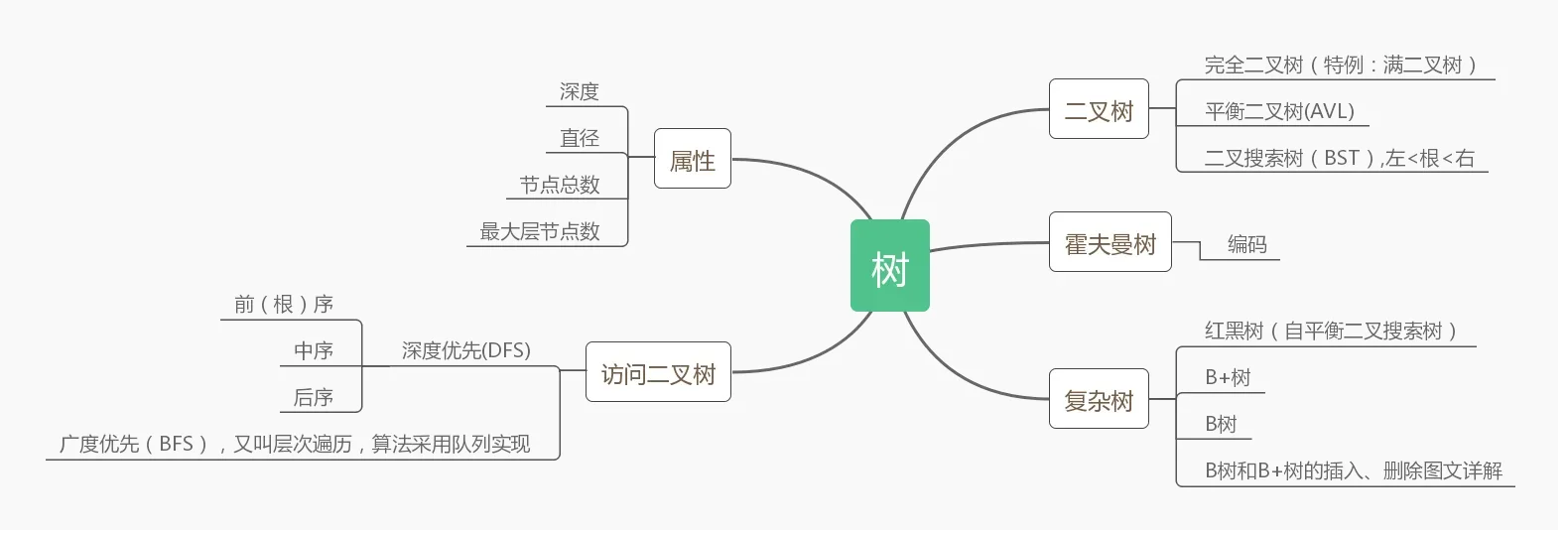
• 其他分类方式
  

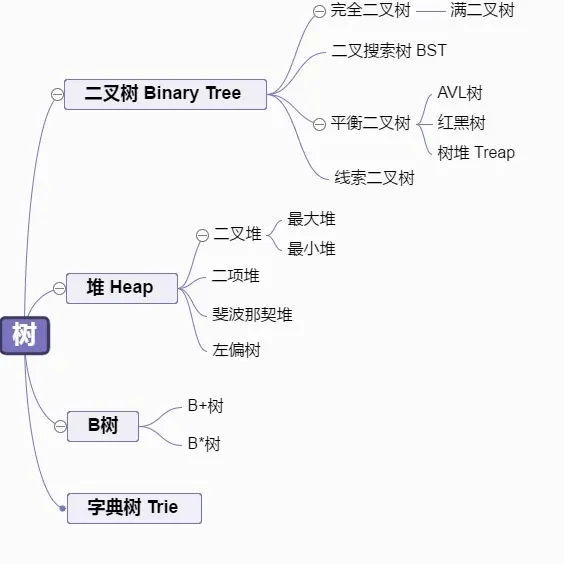
  基础算法

  二叉树的最小深度

  class Solution:
      def minDepth(self, root: TreeNode) -> int:
          if not root:
              return 0
          if root.left==None or root.right==None:
              return self.minDepth(root.left)+self.minDepth(root.right)+1
          else:
              return min(map(self.minDepth,(root.left,root.right)))+1

  完全二叉树中节点的个数

  # 深度遍历(递归法)
  class Solution:
      def countNodes(self, root: TreeNode) -> int:
          return 1+self.countNodes(root.left)+self.countNodes(root.right) if root else 0
  # 广度遍历(层序)
  class Solution:
      def countNodes(self, root: TreeNode) -> int:
          count=0
          if root:
              level=[root]
              while level:
                  count+=len(level)
                  level=[kid for node in level for kid in (node.left,node.right) if kid]
          return count

  二叉树的层平均值

  class Solution:
      def averageOfLevels(self, root: TreeNode) -> List[float]:
          average=[]
          if root:
              level=[root]
              while level:
                  average.append(sum(i.val for i in level)/len(level))
                  level=[kid for node in level for kid in (node.left,node.right) if kid]
          return average

  二叉树的直径

• 采用分治和递归的思想：根节点为root的二叉树的直径 = max(root-left的直径, root->right的直径，root->left的最大深度+root->right的最大深度+1)
• 分两种情况，1，最大直径经过根节点，则直径为左子树最大深度+右子树最大深度 2.如果不经过根节点，则取左子树或右子树的最大深度

  class Solution:
      def diameterOfBinaryTree(self, root: TreeNode) -> int:
          self.diameter=0
          def dfs(root):
              if root==None:
                  return 0
              left=dfs(root.left)
              right=dfs(root.right)
              self.diameter=max(self.diameter,left+right)
              return max(left,right)+1
          dfs(root)
          return self.diameter

  判断二叉树是否是平衡二叉树

• #一般认为平衡二叉树空间复杂度是O(logn)的，这是因为平衡二叉树的高度h就是O(logn)级别的。但是对于一般的树，严谨起见，还是要说O(h)的。这个h可能是logn（最好情况），也可能是n（最坏情况））

  class Solution:
      def isBalanced(self, root: TreeNode) -> bool:
          def check_depth(root):
              if root==None:
                  return 0
              left_depth=check_depth(root.left)
              right_depth=check_depth(root.right)
              return max(left_depth,right_depth)+1
          if root==None:
              return True
          return abs(check_depth(root.left)-check_depth(root.right))<=1 and self.isBalanced(root.left) and self.isBalanced(root.right)

  两个二叉树是否完全相同

  class Solution:
      def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
          if p and q:
              # 两棵二叉树均不为空，如果根节点的值相等，左子树相等和右子树相等，则这两棵二叉树相等，否则不相等。
              return p.val==q.val and self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
          return p is q
  # 最后一句相当于以下两种情况
  if not p and not q: # 两棵树均为空
      return True
  if not p and q or not q and p:  # 两棵树只有一棵为空
      return False

  对称二叉树

  class Solution:
      def isSymmetric(self, root: TreeNode) -> bool:
          def isSym(l,r):
              # 左右节点同时为空
              if not l and not r:
                  return True
              # 左右节点相等，继续递归求解是否为镜像
              if l and r and l.val==r.val:
                  return isSym(l.left,r.right) and isSym(l.right,r.left)
              # 其他情况均不是对称树
              return False
          return isSym(root,root)

  两个二叉树的最低公共祖先节点

  # 思路：递归，如果当前节点就是p或q，说明当前节点就是最近的祖先；如果当前节点不是p或p，就试着从左右子树里找pq；如果pq分别在一左一右被找到，那么当前节点还是最近的祖先返回root就好了；否则，返回它们都在的那一边。
  class Solution:
      def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
          if root==None:   
              return 
          if root==p or root==q:
              return root
          left=self.lowestCommonAncestor(root.left,p,q)
          right=self.lowestCommonAncestor(root.right,p,q)
          if left and right:
              return root
          if left:
              return left
          if right:
              return right
          else:
              return 

  四种遍历方式

• 二叉树的四种遍历方式分别是：前序、中序、后序和层次。它们的时间复杂度都是O(n)，其中n是树中节点个数，因为每一个节点在递归的过程中，只访问了一次。
• 三种深度优先遍历方法的空间复杂度是O(h)，其中h是二叉树的深度，额外空间是函数递归的调用栈产生的，而不是显示的额外变量。空间复杂度，通常是指完成算法所用的辅助空间的复杂度，而不用管算法前置的空间复杂度。比如在树的遍历算法中，整棵树肯定要占O(n)的空间，n是树中节点的个数，这部分空间是“平凡”的，即肯定存在的，我们不讨论它。
• 层次遍历的空间复杂度是O(w)，其中w是二叉树的宽度（拥有最多节点的层的节点数）。
  

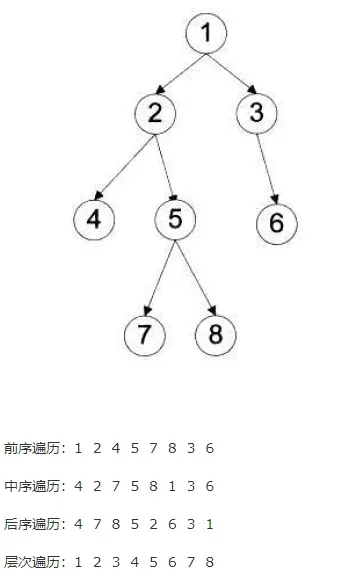
  二叉树的前序遍历

  # 递归解法
  class Solution:
      def preorderTraversal(self, root: TreeNode) -> List[int]:
          ret=[]
          if root:
              ret=ret+[root.val]
              ret=ret+self.preorderTraversal(root.left)
              ret=ret+self.preorderTraversal(root.right)
          return ret
  # 迭代算法思路：使用栈的思想，从根节点开始以此使用ret添加根节点值，stack添加右节点，curr=左节点，如果左节点为None，则获取其上一个右节点（一直输出根节点，添加其右节点，遍历左节点，右节点的输出顺序为从下往上）
  class Solution:
      def preorderTraversal(self, root: TreeNode) -> List[int]:
          ret=[]
          if root==None:
              return ret
          stack=[]
          curr=root
          while curr or stack:
              if curr:
                  ret.append(curr.val)
                  stack.append(curr.right)
                  curr=curr.left
              else:
                  curr=stack.pop()
          return ret

  二叉树的中序遍历

  # 递归解法同上
  # 迭代解法
  class Solution:
      def inorderTraversal(self, root: TreeNode) -> List[int]:
          res=[]
          if root==None:
              return res
          stack=[]  #添加根节点
          curr=root
          while curr or stack:
              if curr:
                  stack.append(curr)
                  curr=curr.left
              else:
                  curr=stack.pop()
                  res.append(curr.val)
                  curr=curr.right
          return res

  二叉树的后序遍历

  # 递归解法同上
  # 迭代算法思路：后序遍历方式为：左右中，将其进行反转 中右左，那么我们可以实现一个中右左，其原理与前序遍历一样
  class Solution:
      def postorderTraversal(self, root: TreeNode) -> List[int]:
          ret=[]
          if root==None:
              return ret
          stack=[]
          curr=root
          while curr or stack:
              if curr:
                  ret.append(curr.val)
                  stack.append(curr.left)
                  curr=curr.right
              else:
                  curr=stack.pop()
          return ret[::-1]

  二叉树的层次遍历

  class Solution:
      def levelOrder(self, root: TreeNode) -> List[List[int]]:
          level=[root]
          ret=[]
          if root==None:
              return []
          while level:
              ret.append([i.val for i in level])
              level=[kid for node in level for kid in (node.left,node.right) if kid]
          return ret

  进阶算法

  不同的二叉树

• 分析：采用动态规划解决，假设用G(n)表示前n个整数的二叉搜索树的总数，F（i）表示 当i节点为根节点的二叉搜索树的个数，当i为根节点时，由于二叉搜索树的规则，前i-1个节点都应该位于以i节点为根节点的左子树，i+1以后的节点都应该位于右子树，那么由咱们的假设可知，由前i-1个节点构成的左子树的二叉搜索树的总数为G(i-1)，同理右子树的二叉搜索树的总数为G（n-i），所以以i为根节点的二叉搜索树的总数F(i) = G(i-1)*G(n-i)，则前n个节点的所有二叉搜索树总数G(n） = F(1)+F(2)+…+F(n)。可以采用动态规划完成。

  class Solution:
      def numTrees(self, n: int) -> int:
          # n=0,n=1的情况
          g=[1,1]
          for i in range(2,n+1):
              f=0
              for j in range(1,i+1):
                  #若i为3：g[0]*g[3]+g[1]*g[2]+g[2]*g[1]+g[3]*g[0]
                  f+=g[j-1]*g[i-j]
              g.append(f)
          return g[-1]

  验证二叉搜索树(BST)

• 一棵BST定义为：节点的左子树中的值要严格小于该节点的值，节点的右子树中的值要严格大于该节点的值，左右子树也必须是二叉查找树，一个节点的树也是二叉查找树。

  class Solution:
      def isValidBST(self, root: TreeNode) -> bool:
          output=[]
          self.inOrder(root,output)
          for i in range(1,len(output)):
              if output[i-1]>=output[i]:
                  return False
          return True
      def inOrder(self,root,output):
          if root==None:
              return
          # 利用中序遍历，自下而上升序排列
          self.inOrder(root.left,output)
          output.append(root.val)
          self.inOrder(root.right,output)

  前序遍历和中序遍历构造二叉树（实现参考）

• 前序的第一个节点必定是根节点，在中序遍历中找到根节点所在的索引x，观察研究可以发现，在中序遍历中根节点索引之前的即为其左孩子，即左孩子们 = root[:x];那么在前序遍历中的左孩子个数和中序遍历是一样的，即为从前序遍历中索引为1（索引0为根节点）到x+1的节点；其余的则为右孩子们。
  最后递归调用自己，得到二叉树

  class Solution:
      def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
          if preorder==[]:
              return None
          # 找到根节点在中序遍历中的位置(索引)
          index=inorder.index(preorder[0])
          root = TreeNode(preorder[0])
          # 递归调用
          root.left=self.buildTree(preorder[1:index+1],inorder[0:index])
          root.right=self.buildTree(preorder[index+1:],inorder[index+1:])
          return root