2022-05-17发表读书笔记24 分钟读完 (大约3535个字)

《深度学习入门：基于Python的理论与实现》

最近想了解下深度学习相关的入门知识，找来找去发现了这本书，从最基础的概念出发，教读者动手实现一个深度学习框架，有基础的高等数学知识后基本可以无障碍阅读。顺便一提，这本书也是日本人写的，跟当初学 C 语言时看柴田望洋的《明解C语言》感觉一样，通俗易懂，尽可能把晦涩的概念讲的简单易懂。

我的新书《LangChain编程从入门到实践》已经开售！推荐正在学习AI应用开发的朋友购买阅读！

感知机（perceptron）

感知机是具有输入和输出的算法，给定一个输入后，将输出一个既定的值，感知机将权重和偏置设定为参数。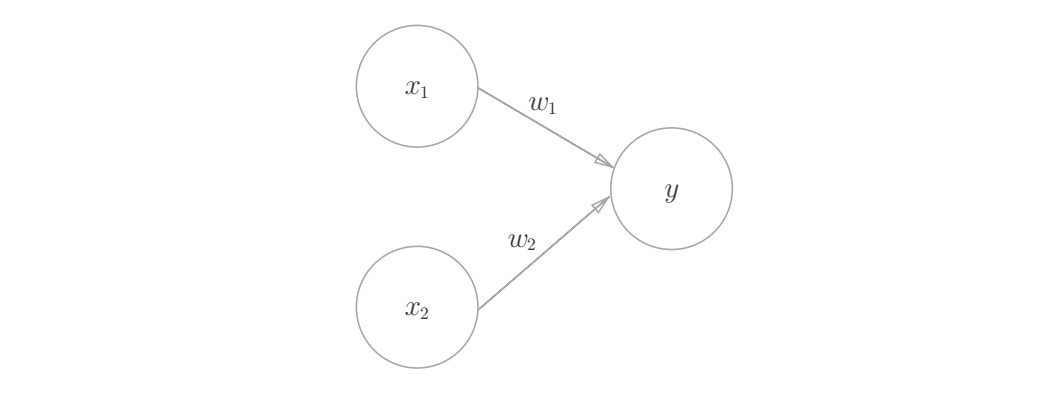

使用感知机可以表示与门和或门等逻辑电路，异或门无法通过单层感知机来表示，但使用2层感知机可以表示异或门，多层感知机（在理论上）可以表示计算机。
单层感知机只能表示线性空间，而多层感知机可以表示非线性空间。

神经网络（neural network）

神经网络中的激活函数使用平滑变化的 sigmoid 函数或 ReLU 函数。神经网络和感知机在信号的按层传递这一点上是相同的，但是向下一个神经元发送信号时，改变信号的激活函数有很大差异，神经网络中使用的是平滑变化的 sigmoid 函数，而感知机中使用的是信号急剧变化的阶跃函数。(感知机神经元之间流动的是0或1的二元信号，而神经网络中流动的是连续的实数值信号。)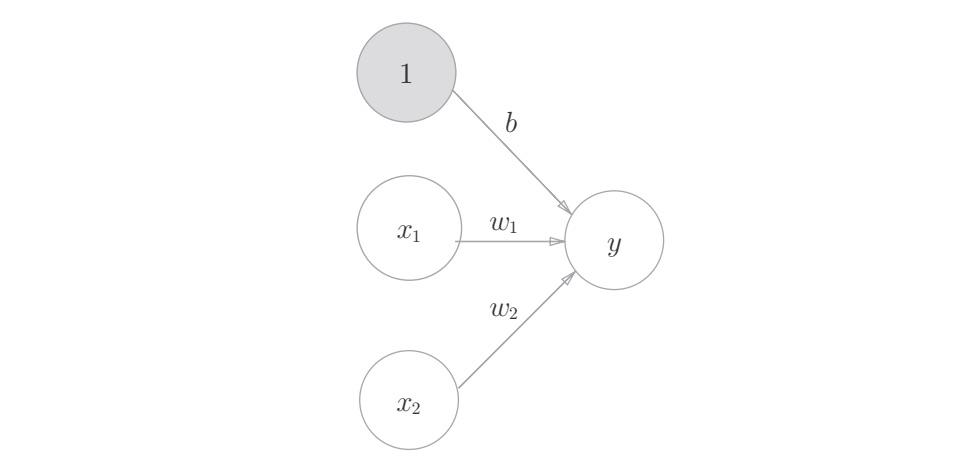

机器学习的问题大体上可以分为回归问题和分类问题，关于输出层的激活函数，回归问题中一般用恒等函数，分类问题中一般用 softmax函数。分类问题中，输出层的神经元的数量设置为要分类的类别数。
输入数据的集合称为批，通过以批为单位进行推理处理，能够实现高速的运算；通过巧妙地使用 NumPy多维数组，可以高效地实现神经网络。

激活函数（activation function）

激活函数的作用在于决定如何激活输入信号的总和。
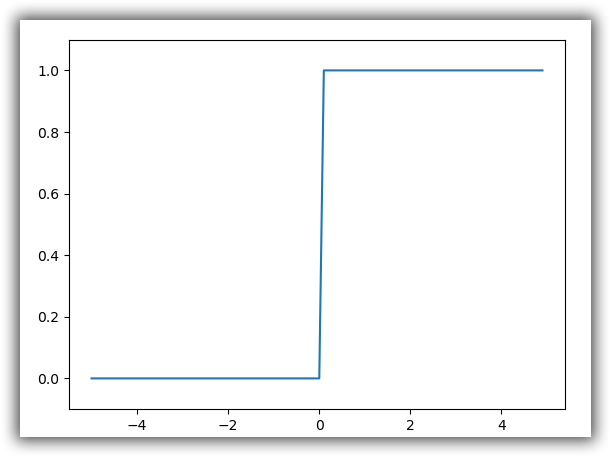
阶跃函数
$$
h(x)=\left{\begin{matrix}
&1 &(x>0) \
&0 &(x<=0)
\end{matrix}\right.
$$

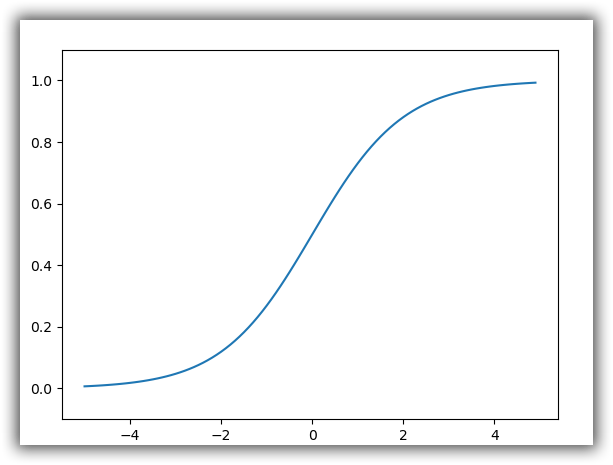
sigmoid 函数

$$
h(x)=\frac{1}{1+exp(-x)}
$$

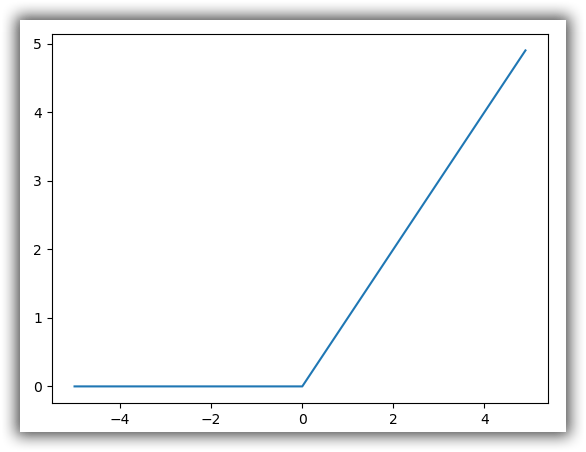
ReLU 函数
$$
h(x)=\left{\begin{matrix}
&x &(x>0) \
&0 &(x<=0)
\end{matrix}\right.
$$

恒等函数
$$
y_{k}=x_{k}
$$
softmax 函数(输出是0到1之间的实数，输出值的总和是1)
$$
y_{k}=\frac{exp(a_{k})}{\sum_{i=1}^{n}exp(a_{i})}
$$

神经网络的学习

机器学习中使用的数据集分为训练数据和测试数据，神经网络用训练数据进行学习，并用测试数据评价学习到的模型的泛化能力。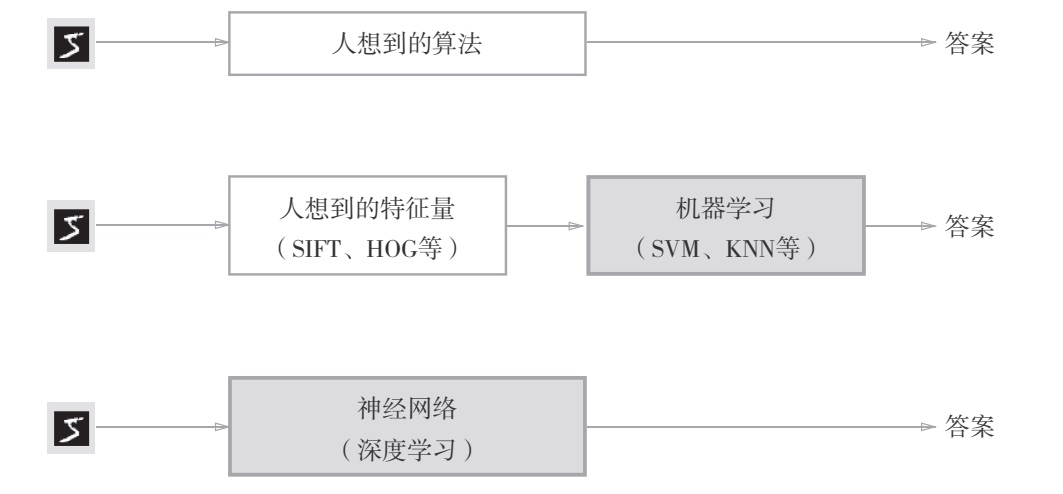

利用某个给定的微小值的差分求导数的过程，称为数值微分，利用数值微分，可以计算权重参数的梯度。

典型损失函数(loss function)

神经网络的学习以损失函数为指标，更新权重参数，以使损失函数的值减小。损失函数可以使用任意函数，但一般用均方误差和交叉熵误差。

均方误差(mean squared error)
$$
E=\frac{1}{2}\sum_{k}(y_{k}-t_{k})^{2}
$$
交叉熵误差(cross entropy error)
$$
E=-\sum_{k}t_{k}logy_{k}
$$

梯度法(gradient)

梯度法：梯度的负方向并不一定指向最小值，但沿着它的方向能够最大限度地减小函数的值，通过（不断调整梯度方向）不断地沿梯度方向前进，逐渐减小函数值的过程称为梯度法。寻找最小值的梯度法称为梯度下降法，寻找最大值称为梯度上升法。对随机选择的 mini batch 数据进行的梯度下降法称为SGD(stochastic gradient descent)。
$$
x0=x0-\eta \frac{\partial f}{\partial x_{0}}
$$
$$
x1=x1-\eta \frac{\partial f}{\partial x_{1}}
$$
$\eta$表示更新量，在神经网络学习中称为学习率(learning rate),学习率决定在一次学习中应该学习多少，以及在多大程度上更新参数。学习率属于超参数，需要人工设定。

误差反向传播法

神经网络的损失是输入和网络参数的函数，取一批训练样本作为输入，把参数视为变量，可以对它们求导。损失函数再复杂（神经网络层数越多，损失函数越复杂）也是若干仿射变换、激活函数以及softmax的叠加。利用链式法则，我们总能把导函数求出来。但是求解过程费时费力，并且随着神经网络加深变得越发艰难，不同的网络有不一样的导数，每次创建新网络都要计算一次导函数，不能一劳永逸地解决问题。
根据链式法则，一个量A关于另一个量W的导数与W是怎么计算出来的无关，又由于神经网络同一层的神经元执行相同的运算（因此具有相同形式的局部导数（这一层的输出关于这一层的输入（也许这是上一层的输出）的导数）），我们可以让层记忆与求局部导数相关的计算（做预测）的中间结果，再从后往前（从输出向输入）逐层逐中间变量计算导数，最终得到损失关于输入的导数。具体理解参考 3Blue1Brown
通过使用计算图，可以直观地把握计算过程，计算图的节点是由局部计算构成的，局部计算构成全局计算，计算图的正向传播进行一般的计算，通过计算图的反向传播，可以计算各个节点的导数。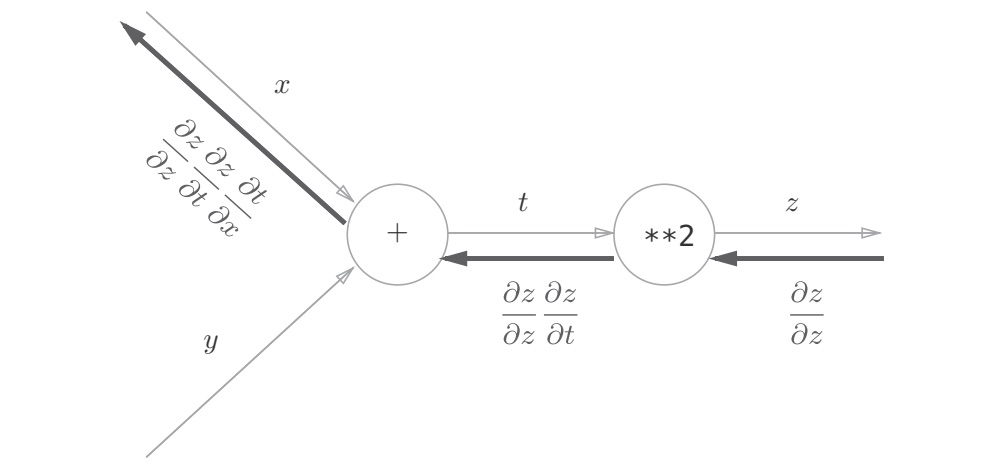

通过比较数值微分和误差反向传播法的结果，可以确认误差反向传播法的实现是否正确（这一过程称作梯度确认）。

与学习相关的技巧

寻找最优权重参数的最优化方法

除了SGD之外，还有 Momentum、 AdaGrad（会为参数的每个元素适当的调整学习率）、Adam等方法。最优化方法的比较: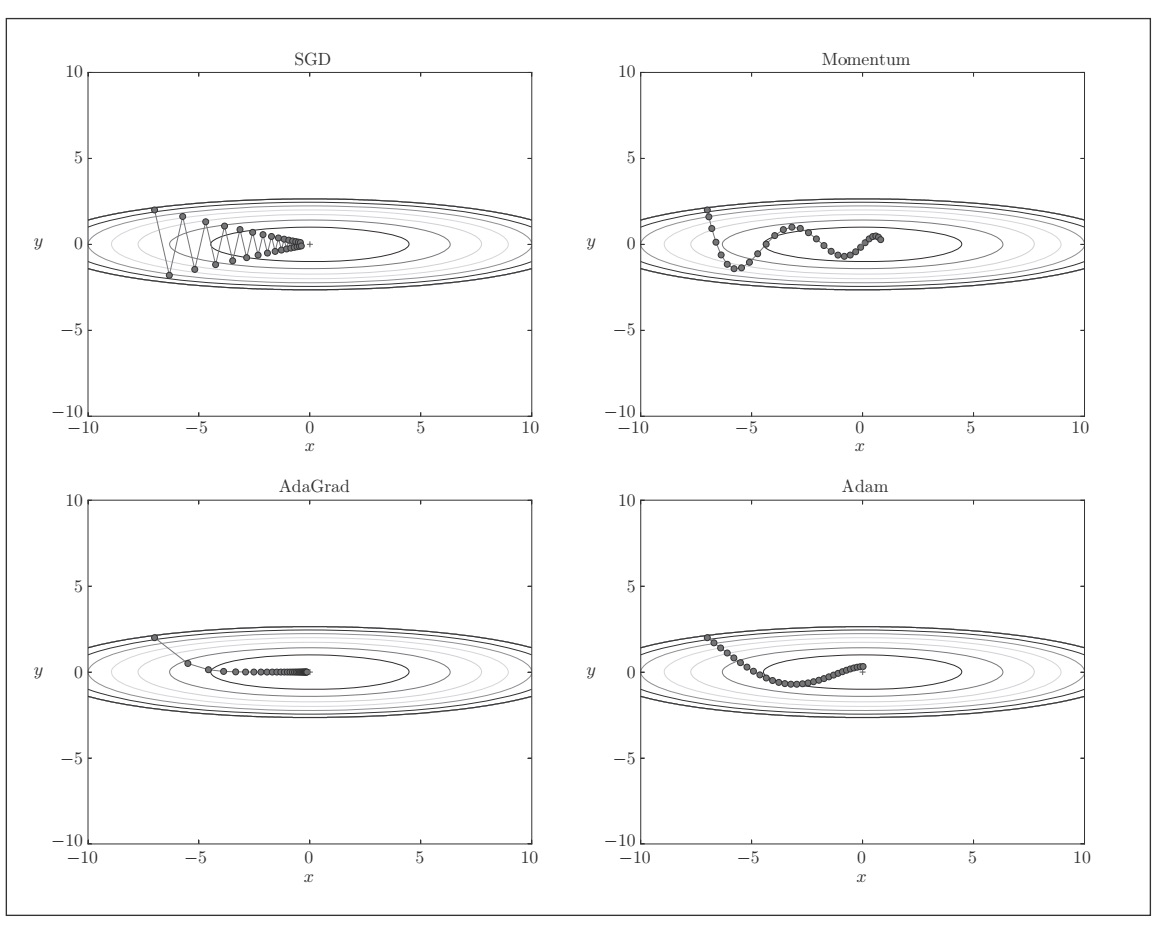

权重参数的初始值

各层的激活值的分布都要求有适当的广度。因为通过在各层间传递多样性的数据，神经网络可以进行高效的学习。反过来，如果传递的是有所偏向的数据，就会出现梯度消失或者“表现力受限”的问题，导致学习可能无法顺利进行。所以权重初始值的赋值方法对进行正确的学习非常重要。作为权重初始值， Xavier初始值、He初始值等比较有效。
通过使用 Batch Normalization（以进行学习时的mini-batch为单位，按mini-batch进行正规化，具体就是进行使数据分布的均值为0、方差为1的正规化。），“强制性”地调整激活值的分布，可以加速学习，并且对初始值变得健壮（不依赖于初始值）。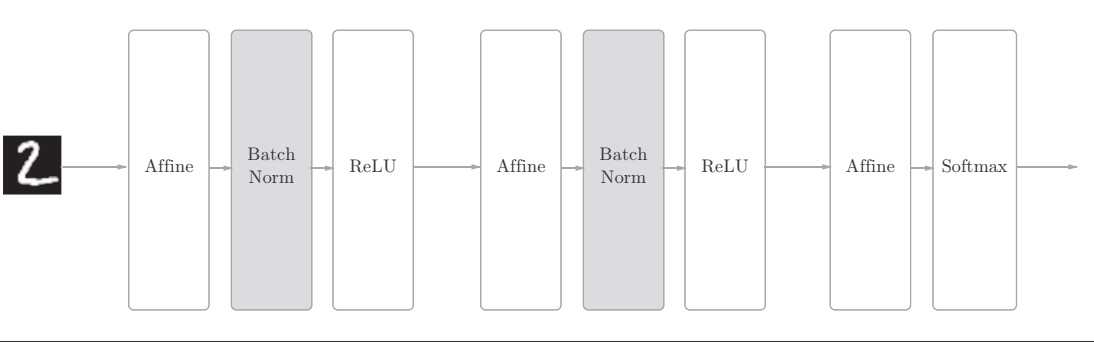

抑制过拟合

过拟合指的是只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。权值衰减是一直以来经常被使用的一种抑制过拟合的方法，该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合，很多过拟合原本就是因为权重参数取值过大才发生的。
Dropout是一种在学习的过程中随机删除神经元的方法。训练时，每传递一次数据，就会随机选择要删除的神经元，被删除的神经元不再进行信号的传递。然后，测试时虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。

超参数的最优化

超参数是指各层的神经元数量、 batch大小、参数更新时的学习率或权值衰减等。训练数据用于参数（权重和偏置）的学习，验证数据用于超参数的性能评估。为了确认泛化能力，要在最后使用（比较理想的是只用一次）测试数据。

步骤：设定超参数的范围；从设定的超参数范围中随机采样；使用采样到的超参数的值进行学习，通过验证数据评估识别精度（但是要将epoch设置得很小）；重复大约100次，根据它们的识别精度的结果，缩小超参数的范围。反复进行上述操作，不断缩小超参数的范围，在缩小到一定程度时，从该范围中选出一个超参数的值。

卷积神经网络

基于全连接层（Affine层）的网络，神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换” ，这里将进行仿射变换的处理实现为“Affine层”。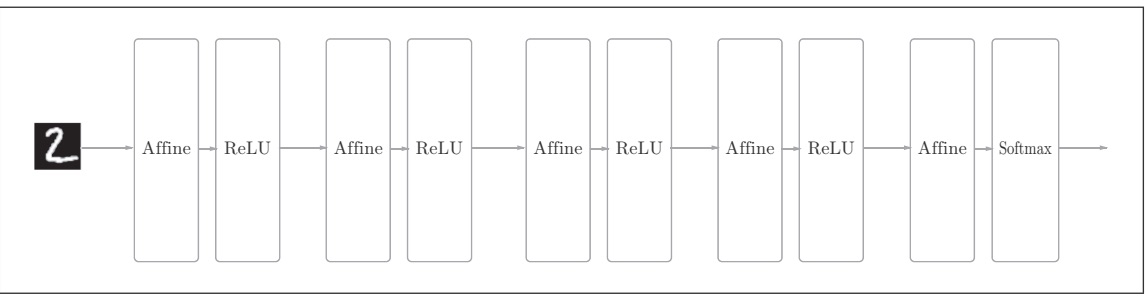

基于CNN的网络：新增了Convolution层和Pooling层(使用im2col函数可以简单、高效地实现卷积层和池化层。)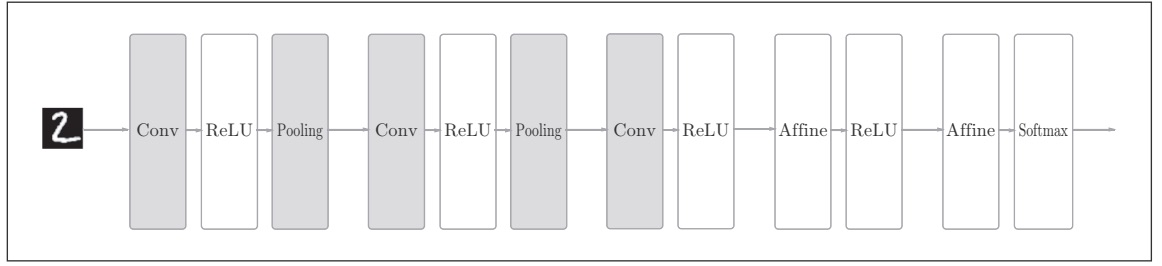

卷积层

卷积运算

卷积层的输入数据称为输入特征图（input feature map），输出数据称为输出特征图（output feature map），卷积层进行的处理就是卷积运算。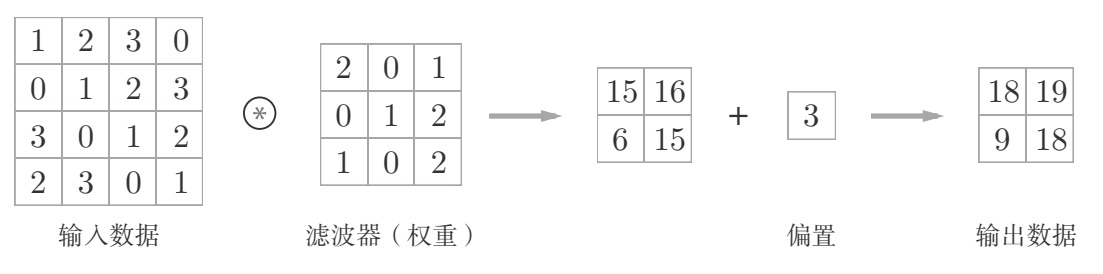

填充

卷积运算的填充处理：向输入数据的周围填入0（图中用虚线表示填充，并省略了填充的内容“ 0”），卷积运算就可以在保持空间大小不变的情况下将数据传给下一层。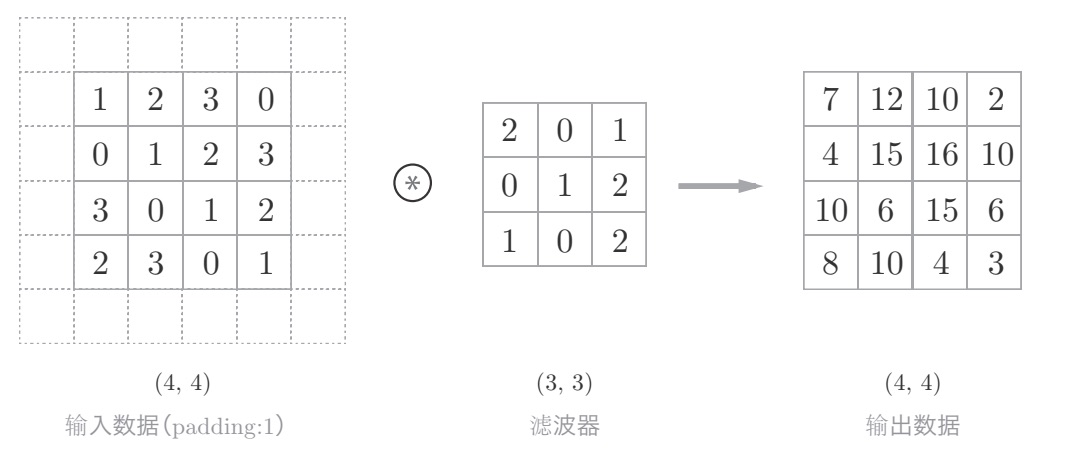

步幅

应用滤波器的位置间隔称为步幅（stride）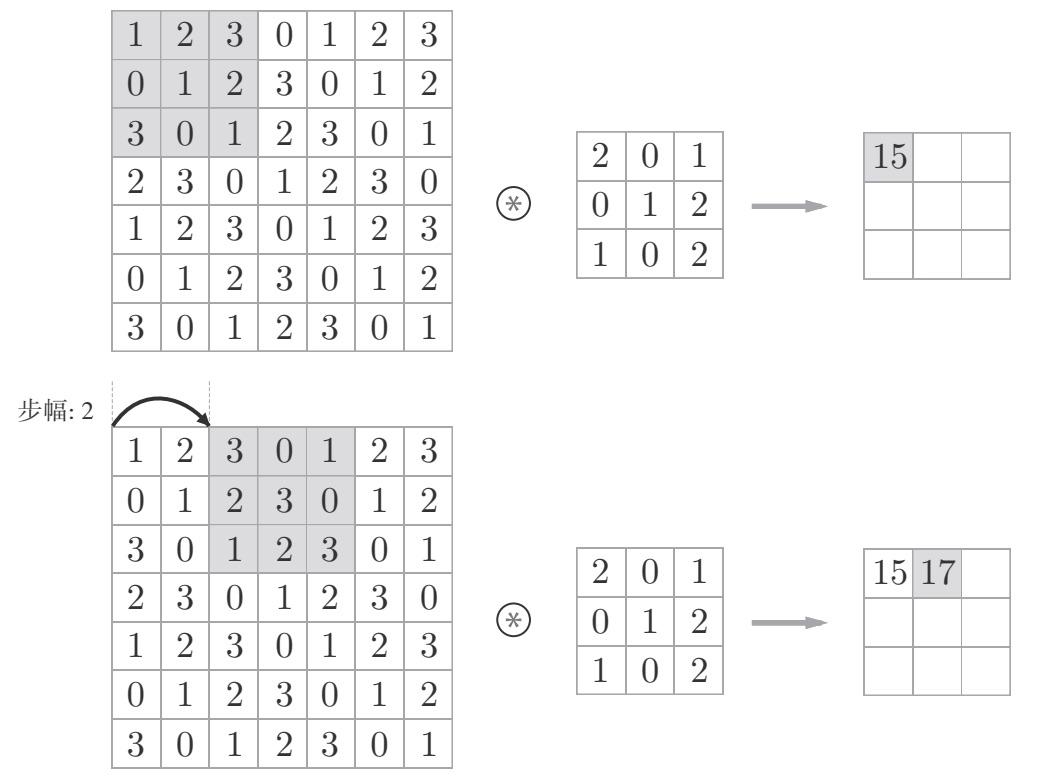

批处理

卷积运算必须考虑滤波器的数量。因此，作为4维数据，滤波器的权重数据要按(output_channel, input_channel , height, width)的顺序书写。比如，通道数为3、大小为5 × 5的滤波器有20个时，可以写成(20, 3, 5, 5)。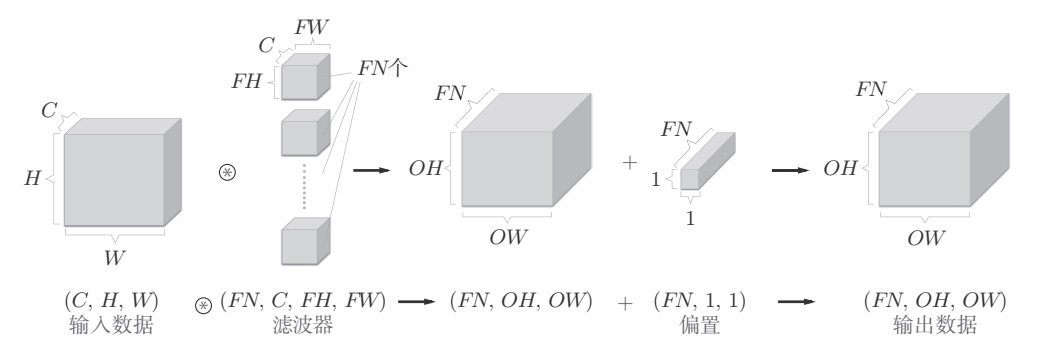

卷积运算的处理流（批处理），按(batch_num, channel, height, width)的顺序保存数据。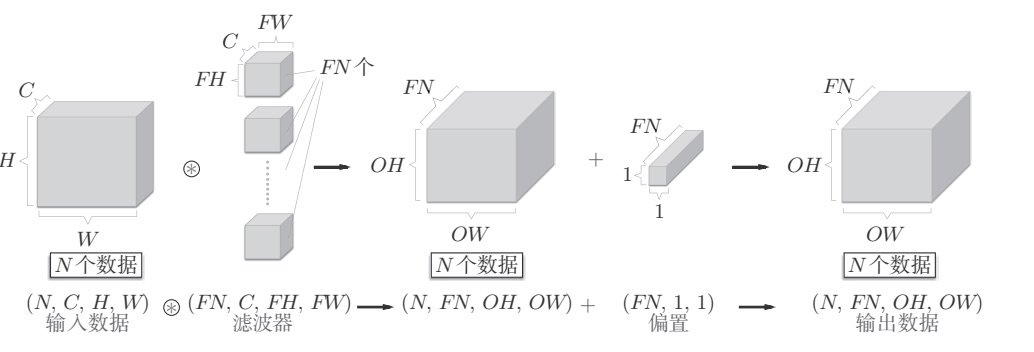

池化层

池化只是从目标区域中取最大值（或者平均值），所以不存在要学习的参数。经过池化运算，输入数据和输出数据的通道数不会发生变化，计算是按通道独立进行的。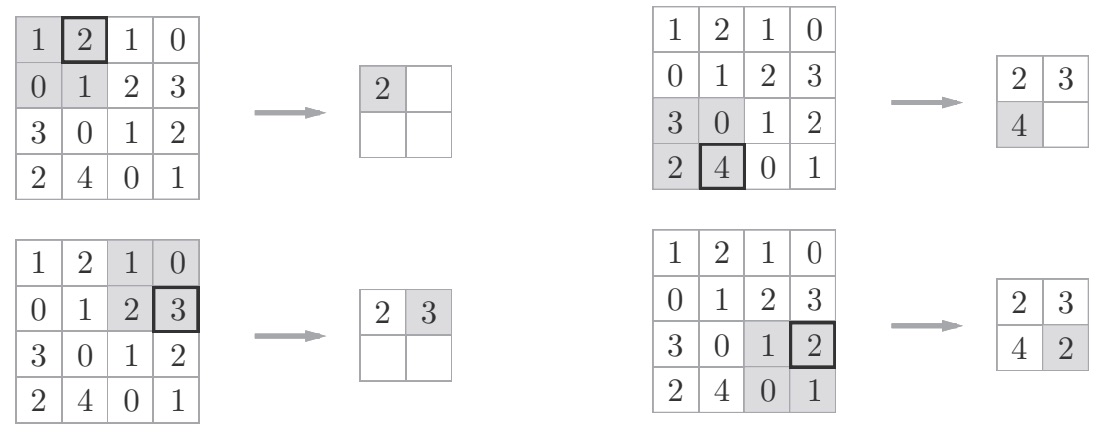

除了Max池化之外，还有Average池化等。相对于Max池化是从目标区域中取出最大值，Average池化则是计算目标区域的平均值。在图像识别领域，主要使用Max池化。

深度学习

在深度学习的发展中，大数据和GPU做出了很大的贡献，对于大多数的问题，都可以期待通过加深网络来提高性能。基于GPU、分布式学习、位数精度的缩减，可以实现深度学习的高速化。深度学习（神经网络）不仅可以用于物体识别，还可以用于物体检测、图像分割，深度学习的应用包括图像标题的生成、图像的生成、强化学习。